Lumos Video Store
This page provides a list of educational videos related to Add or Subtract 0 or 1. You can also use this page to find sample questions, apps, worksheets, lessons , infographics and presentations related to Add or Subtract 0 or 1.
Quadratic Word Problems | MathHelp.com

By MathHelp.com
A number is 56 less than its square. Find the number. To solve this problem, let’s translate the first sentence into an equation. A number, that’s x, is, =, 56 less than it’s square, that’s x squared – 56. Remember that “less than” switches the order around. In other words, “56 less than its square” is not 56 minus x squared, it’s x squared minus 56. Next, since we have an x squared term in our equation, we set it equal to 0 by subtracting x from both sides, and we have 0 = x squared – x – 56. Next, we factor the right side as the product of two binomials. In the first position of each binomial, we have the factors of x squared, x and x. In the second position of each binomial, we’re looking for the factors of -56 that add to -1, which are -8 and positive 7. So we have 0 = x - 8 times x + 7, which means that either 0 = x – 8 or 0 = x + 7. Finally, in the first equation, we add 8 to both sides, to get 8 = x. And in the second equation, we subtract 7 from both sides, to get -7 = x. So 8 = x or -7 = x. It’s important to understand that both of these answers work. Plugging an 8 back into the original problem, we have 8 is 56 less than 8 squared, or 8 = 8 squared – 56, which simplifies to 8 = 64 – 56, or 8 = 8, which is a true statement. And plugging a -7 back into the original problem, we have -7 is 56 less than -7 squared, or -7 = -7 squared – 56, which simplifies to -7 = 49 – 56, or -7 = -7, which is also a true statement.
Adding and Subtracting Polynomials | MathHelp.com

By MathHelp.com
In this example, notice that each of our variables, x, y, and z, appears in all three equations. To solve this system, we use the addition method. In other words, let’s start with our first two equations, x + y + z = 4, and x – y + z = 2. Notice that if we add these equations together, the +y and –y will cancel out, and we have 2x + 2z = 6. So, in our new equation, 2x + 2z = 6, we’ve eliminated the variable y. Unfortunately, we still haven’t solved for any of our variables. However, if we can create another equation with just x and z in it, then we’ll have a system of equations in two variables, which we can use to solve for x and z. To create another equation with just x and z in it, we need to eliminate y. We can’t add the first and second equations together, because we’ve already done that. However, notice that if we add the first and third equations together, the first equation has a +y and the third equation has a –y, so we’ll be able to eliminate the y. So we have our first equation, x + y + z = 4, and our third equation, x – y – z = 0, and adding them together, notice that the +y – y cancels out, and, as a bonus, the +z – z also cancels out, so we have 2x = 4, and dividing both sides by 2, x = 2. Now, since we know that x = 2, notice that if we plug a 2 in for x in the equation that we created earlier, we can solve for z. And we have 2(2) + 2z = 6, or 4 + 2z = 6, and subtracting 4 from both sides, we have 2z = 2, and dividing both sides by 2, z = 1. So x = 2 and z = 1, and to find the value of y, we simply plug our values of x and z into any of the equations in the original system. Let’s use the first equation, x + y + z = 4. Since x = 2 and z = 1, we plug a 2 in for x and a 1 in for z, and we have 2 + y + 1 = 4, or 3 + y = 4, and subtracting 3 from both sides, y = 1. So x = 2, y = 1, and z = 1, and finally, we write our answer as the ordered triple, x, y, z, or (2, 1, 1).
Work Word Problems | MathHelp.com

By MathHelp.com
To solve a polynomial inequality, like the one shown here, our first step is to write the corresponding equation. In other words, we simply change the inequality sign to an equals sign, and we have x^2 – 3 = 9 – x. Next, we solve the equation. Since we have a squared term, we first set the equation equal to 0. So we move the 9 – x to the left side by subtracting 9 and adding x to both sides of the equation. This gives us x^2 + x – 12 = 0. Next, we factor the left side as the product of two binomials. Since the factors of negative 12 that add to positive 1 are positive 4 and negative 3, we have x + 4 times x – 3 = 0. So either x + 4 = 0 or x – 3 = 0, and solving each equation from here, we have x = -4, and x = 3. Now, it’s important to understand that the solutions to the equation, -4 and 3, represent what are called the “critical values” of the inequality, and we plot these critical values on a number line. However, notice that our original inequality uses a greater than sign, rather than greater than or equal to sign, so we use open dots on our critical values of -4 and positive 3. Remember that ‘greater than’ or ‘less than’ means open dot, and ‘greater than or equal to’ or ‘less than or equal to’ means closed dot. Now, we can see that our critical values have divided the number line into three separate intervals: less than -4, between -4 and 3, and greater than 3. And here’s the important part. Our next step is to test a value from each of the intervals by plugging the value back into the original inequality to see if it gives us a true statement. So let’s first test a value from the “less than -4” interval, such as -5. If we plug a -5 back in for both x’s in the original inequality, we have -5 squared – 3 greater than 9 minus a -5, which simplifies to 25 – 3 greater than 9 + 5, or 22 greater than 14. Since 22 greater than 14 is a true statement, this means that all values in the interval we’re testing are solutions to inequality, so we shade the interval. Next, we test a value from the “between -4 and 3” interval, such as 0. If we plug a 0 back in for both x’s in the original inequality, we have 0 squared – 3 greater than 9 – 0, which simplifies to 0 – 3 greater than 9, or -3 greater than 9. Since -3 greater than 9 is a false statement, this means that all values in the interval we’re testing are not solutions to inequality, so we don’t shade the interval. Next, we test a value from the “greater than 3” interval, such as 4. If we plug a 4 back in for both x’s in the original inequality, we have 4 squared – 3 greater than 9 – 4, which simplifies to 16 – 3 greater than 5, or 13 greater than 5. Since 13 greater than 5 is a true statement, this means that all values in the interval we’re testing are solutions to inequality, so we shade the interval. Finally, we write the answer that’s shown on our graph in set notation. The set of all x’s such that x is less than -4 or x is greater than 3.
Area Between Two Curves

By The Organic Chemistry Tutor
This calculus video tutorial provides a basic introduction in finding the area between two curves with respect to y and with respect to x. It explains how to set up the definite integral to calculate the area of the shaded region bounded by the two curves. In order to find the points of intersection, you need to set the two curves equal to each other and solve for x or y. You need to be familiar with some basic integration techniques for this lesson. This video contains plenty of examples and practice problems.
3rd Grade Math Rap

By McCarthy Math Academy
With a little help from the group, Mindless Behavior, I have created a math video with lyrics to help my students to understand and apply core math skills for third grade. People of all ages can jam out to this one. Enjoy!
I've got a case of the operation blues.
Because I don't know which one I should use.
Look at the word problem for the clues.
The key words tell you how to choose.
Each means you multiply or you must divide.
Tryna find the total? Then you multiply
Total's in the problem? Then you must divide.
Not quick to solve it, draw it, get it right.
Addition's easy for me and you
Sum, In all, together, and total too.
When do you subtract? How many more?
Fewer? Left? Less? Difference in a score?
Place value's next. Disco on the " dess "
Ones, tens, hundreds, to the left
Thousands, Ten thousands, hundred...thousand
Say the name of the place, yeah.
The value's the amount of the place
For example, 2,060.
The value of the 2 is 2-0-0-0,
The value of the 6 is 6-0.
When you round, find and underline the place
Spotlight to the right, decide the digit's fate
5 or more, add 1 to the rounding place
4 or less, do nothing but walk away, (estimate)
A pen, penny is one, one cent
A Nic-kel is five, a dime is ten cents
25 for a quarter, George Washington
100 cents makes a dollar, there he goes again.
For pictographs, you gotta check out the key
One smiley face might really equal three
For bar graphs, pay attention to the scale
Think it's counting by ones, huh, you'll fail
Fractions are easy, just draw your best.
Here they go from least to greatest
1/12, 1/6, ¼, 1/3,
½, 2/3, ¾, Fraction nerd!
You see that number on top,
That's called the numerator
It describes the amount
That is being considered
And if you jump down from the fraction bar
Denominator
It's the total number of equal parts.
Let me give you an example:
Leslie Moin has some coins
A total of 9
2 happen to be pennies
While 7 are dimes.
What's the fraction of dimes?
How many coins? 9
How many dimes? 7
Say the fraction -- seven ninths
Length times width is Area
Distance around is Perimeter
Break down the GEOMETRY
3 sides makes triangle
4 sides = quadrilateral
5 pentagon, 6 hexagon
8 octagon, 10 decagon
Lines that never cross - PARALLEL
Lines that meet or cross - INTERSECTING
Lines that form right angles -- PERPENDICULAR
Same shape, same size -- CONGRUENT
Line that cuts in half - SYMMETRY
Up and Down - VERTICAL
Left to Right -- HORIZONTAL
An angle less than right - ACUTE
An angle opened wide - OBTUSE
Ninety degrees square corner - RIGHT ANGLE
Back to triangles
3 sides the same = equilateral
2 sides the same = isosceles
no sides the same = Hey, that's a scalene right!
So, that's it.
That's our math song.
Before we leave,
Remember to read
Your math problems three times before you answer.
That way you know what the problem
Is asking you to do.
Don't be lazy, be brilliant.
Piece! Like a fraction.
10 - Series and Sigma Summation Notation - Part 1 (Geometric Series & Infinite Series)

By Math and Science
Quality Math And Science Videos that feature step-by-step example problems!
Integration By Partial Fractions

By The Organic Chemistry Tutor
This calculus video tutorial provides a basic introduction into integrating rational functions using the partial fraction decomposition method. Partial fraction decomposition is the process of breaking a single complex fraction into multiple simpler fractions. The integrals of many rational functions lead to a natural log function with absolute value expressions. This video explains what to do when you have repeated linear factors and quadratic factors. This tutorial contains many examples and practice problems on integration by partial fractions.
08 - Learn Synthetic Division of Polynomials - Part 1

By Math and Science
Quality Math And Science Videos that feature step-by-step example problems!
04 - What is the Unit Circle? Angle Measure in Degrees, Reference Angles & More.
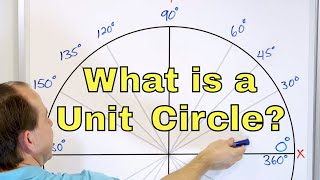
By Math and Science
Quality Math And Science Videos that feature step-by-step example problems!
06 - Graphing Parabolas - Shifting Vertically (Quadratic Functions)

By Math and Science
Quality Math And Science Videos that feature step-by-step example problems!
05 - Polynomial Long Division - Part 1 (Division of Polynomials Explained)

By Math and Science
Quality Math And Science Videos that feature step-by-step example problems!








