Lumos Video Store
This page provides a list of educational videos related to Solving Systems Using Elimination. You can also use this page to find sample questions, apps, worksheets, lessons , infographics and presentations related to Solving Systems Using Elimination.
Ex 2: Solve a System of Equations Using the Elimination Method

By Mathispower4u
Ex 2: Solve a System of Equations Using the Elimination Method
SAT Math Part 7 - Solving Systems of Equations Using Elimination & Substitution - Membership
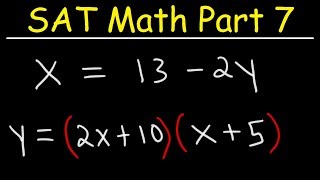
By The Organic Chemistry Tutor
Adding and Subtracting Polynomials | MathHelp.com

By MathHelp.com
In this example, notice that each of our variables, x, y, and z, appears in all three equations. To solve this system, we use the addition method. In other words, let’s start with our first two equations, x + y + z = 4, and x – y + z = 2. Notice that if we add these equations together, the +y and –y will cancel out, and we have 2x + 2z = 6. So, in our new equation, 2x + 2z = 6, we’ve eliminated the variable y. Unfortunately, we still haven’t solved for any of our variables. However, if we can create another equation with just x and z in it, then we’ll have a system of equations in two variables, which we can use to solve for x and z. To create another equation with just x and z in it, we need to eliminate y. We can’t add the first and second equations together, because we’ve already done that. However, notice that if we add the first and third equations together, the first equation has a +y and the third equation has a –y, so we’ll be able to eliminate the y. So we have our first equation, x + y + z = 4, and our third equation, x – y – z = 0, and adding them together, notice that the +y – y cancels out, and, as a bonus, the +z – z also cancels out, so we have 2x = 4, and dividing both sides by 2, x = 2. Now, since we know that x = 2, notice that if we plug a 2 in for x in the equation that we created earlier, we can solve for z. And we have 2(2) + 2z = 6, or 4 + 2z = 6, and subtracting 4 from both sides, we have 2z = 2, and dividing both sides by 2, z = 1. So x = 2 and z = 1, and to find the value of y, we simply plug our values of x and z into any of the equations in the original system. Let’s use the first equation, x + y + z = 4. Since x = 2 and z = 1, we plug a 2 in for x and a 1 in for z, and we have 2 + y + 1 = 4, or 3 + y = 4, and subtracting 3 from both sides, y = 1. So x = 2, y = 1, and z = 1, and finally, we write our answer as the ordered triple, x, y, z, or (2, 1, 1).
Systems of Three Equations | MathHelp.com

By MathHelp.com
Here we’re asked to graph the following function and use the horizontal line test to determine if it has an inverse. And if so, find the inverse function and graph it. So let’s start by graphing the given function, f(x) = 2x – 4, and remember that f(x) is the same as y, so we can rewrite the function as y = 2x – 4. Now, we simply graph the line y = 2x – 4, which has a y-intercept of -4, and a slope of 2, or 2/1, so we go up 2 and over 1, plot a second point and graph our line, which we’ll call f(x). Next, we’re asked to use the horizontal line test to determine if the function has an inverse. Since there’s no way to draw a horizontal line that intersects more than one point on the function, the function does have an inverse. So we need to find the inverse and graph it. To find the inverse, we switch the x and the y in original function, y = 2x – 4, to get x = 2y – 4. Next, we solve for y, so we add 4 to both sides to get x + 4 = 2y, and divide both sides by 2 to get 1/2x + 2 = y. Next, let’s flip our equation so that y is on the left side, and we have y = 1/2x + 2. Finally, we replace y with the notation that we use for the inverse function of f, as shown here. And remember that we’re asked to graph the inverse as well, so we graph y = ½ x + 2. Our y-intercept is positive 2, and our slope is ½, so we go up one and over 2, plot a second point, graph the line, and label it as the inverse function of f. Notice that the graph of the inverse function is a reflection of the original function in the line y = x.
14 - Solve Quadratic Systems of Equations by Addition - Part 1 (Simultaneous Equations)

By Math and Science
Quality Math And Science Videos that feature step-by-step example problems!
12 - Solving 3-Variable Linear Systems of Equations - Substitution Method

By Math and Science
Quality Math And Science Videos that feature step-by-step example problems!
Addition elimination method 3 | Systems of equations | 8th grade | Khan Academy

By Khan Academy
Khan Academy presents Addition Elimination Method 3, an educational video resource on math.
Autism: An evolutionary perspective, Professor Simon Baron-Cohen, 1st Symposium of EPSIG, 2016

By Lumos Learning
First Symposium of the Evolutionary Psychiatry Special Interest Group of the Royal College of Psychiatrists, Oct 4th 2016 in London. Lecture by Professor Simon Baron-Cohen from Cambridge University Autism Research Centre.



