Lumos Video Store
This page provides a list of educational videos related to Hands On: Circles. You can also use this page to find sample questions, apps, worksheets, lessons , infographics and presentations related to Hands On: Circles.
Basic information about circles

By MathPlanetVideos
What's the angle of the circle arc if we divide a cicle in 12 equally sized pieces
11.6 Areas of Circles, Sectors & Segments (Lesson)

By AutenMath
A lesson on finding the area of circles, sectors and segments
Partitioning Circles and Rectangles: 2.G.3

By Tenmarks Amazon
Students learn to create and discuss halves, thirds, and fourths of circles and rectangles.
Partitioning Circles and Rectangles: 2.G.3

By Tenmarks Amazon
Students learn to create and discuss halves, thirds, and fourths of circles and rectangles.
Partitioning rectangles, squares, and circles into halves and fourths-2nd grade

By Tyris Hall
Partitioning rectangles into halves
Math-U-See Geometry - Homeschooling Help Circles Inscribed Angles - TabletClass.com
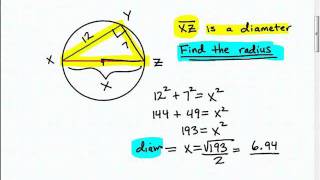
By TabletClass Math
Youtube Presents Math-U-See Geometry - Homeschooling Help Circles Inscribed Angles - TabletClass.com an educational video resources on math
Equation for a circle using the Pythagorean Theorem | Circles | Geometry | Khan Academy

By Khan Academy
Equation for a circle using the Pythagorean Theorem | Circles | Geometry | Khan Academy
Tangents and Circles - YourTeacher.com - Geometry Help

By yourteachermathhelp
Students learn the following theorems related to tangents. If a line is tangent to a circle, then the line is perpendicular to the radius at the point of tangency. If a line is perpendicular to a radius at its outer endpoint, then the line is tangent to the circle. If two tangent segments are drawn to a circle from an external point, then the tangent segments are congruent. Students are then asked to use these theorems to find missing segment lengths and missing angle measures in given figures. Students also learn the definitions of common internal tangents and common external tangents.
Pythagorean theorem and the equation of a circle

By Khan Academy
Pythagorean theorem and the equation of a circle
Pythagorean theorem and the equation of a circle

By Khan Academy
Pythagorean theorem and the equation of a circle
Area of inscribed equilateral triangle (some basic trig used) | Circles | Geometry | Khan Academy

By Khan Academy
This video will give you a good feel for what inscribed figures are like. It uses some trigonometry to figure out what the area of an equilateral triangle inscribed in a circle is, given the circle's radius. NOTE: We don't actually need trigonometry to solve this problem. Notice that we can view the equilateral triangle as six identical 30-60-90 triangles, the hypotenuses of which are radii of the circle, then use the 30-60-90 triangle side length ratios to figure out the rest of what we need to know to solve the problem.
Area of inscribed equilateral triangle (some basic trig used) | Circles | Geometry | Khan Academy

By Khan Academy
This video will give you a good feel for what inscribed figures are like. It uses some trigonometry to figure out what the area of an equilateral triangle inscribed in a circle is, given the circle's radius. NOTE: We don't actually need trigonometry to solve this problem. Notice that we can view the equilateral triangle as six identical 30-60-90 triangles, the hypotenuses of which are radii of the circle, then use the 30-60-90 triangle side length ratios to figure out the rest of what we need to know to solve the problem.
Inscribing and circumscribing circles on a triangle

By Khan Academy
Inscribing and circumscribing circles on a triangle
Proof: Right triangles inscribed in circles | High School Math | Khan Academy

By Khan Academy
Proof showing that a triangle inscribed in a circle having a diameter as one side is a right triangle. All Khan Academy content is available for free at www.khanacademy.org
Circles: radius, diameter, circumference and Pi | Geometry | Khan Academy

By Khan Academy
The radius is the distance between the center and any point on the circumference of a circle. The diameter is always twice the radius. The circumference is the perimeter of the circle.
Circle: Application: Finding Area and Length of a Race Track

By easymathk12
An oval track is made by erecting semicircles on each end of a 60m by 120m rectangle. Find the length of the track and the area enclosed by the track.

