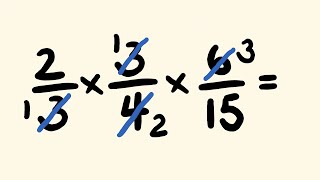Lumos Video Store
This page provides a list of educational videos related to Divide by 9 and 10. You can also use this page to find sample questions, apps, worksheets, lessons , infographics and presentations related to Divide by 9 and 10.
Dividing Scientific Notation | MathHelp.com

By MathHelp.com
To multiply numbers that are in written in scientific notation, such as 1.4 x 10 to the -2nd times 5.3 times 10 to the 6th, we first multiply the decimals, in this case 1.4 times 5.3, to get 7.42. Next, we multiply the powers of 10, in this case 10 to the -2nd times 10 to the 6th. Notice that we’re multiplying two powers that have like bases, so we add the exponents and leave the base the same, to get 10 to the -2 + 6, or 10 to the 4th. So we have 7.42 times 10 to the 4th. Finally, we’re asked to write our answer in scientific notation. Notice, however, that 7.42 times 10 to the -4th is already written in scientific notation, because we have a decimal between 1 and 10 that is multiplied by a power of 10. So we have our answer.
04 - Simplify Fractions to Lowest Terms (Simplifying & Reducing Fractions) - Part 2

By Math and Science
Quality Math And Science Videos that feature step-by-step example problems!
Learn Simplifying Fractions & Equivalent Fractions - [5-4-13]

By Math and Science
Quality Math And Science Videos that feature step-by-step example problems!